Warren McCulloch and Walter Pitts‘
seminal work, “A Logical Calculus of the Ideas Immanent in Nervous Activity.” Published in 1943, this paper laid the foundation for neural network theory and computational neuroscience. It introduced the concept of artificial neural networks and explored how the brain could be represented using logical and mathematical operations.
A Logical Calculus of the Ideas Immanent in Nervous Activity” is a groundbreaking research paper that proposed a mathematical framework for understanding the functioning of the nervous system and laid the groundwork for artificial neural networks.

Here’s an overview of the key ideas and contributions
Neurons as Logical Elements: The paper suggested that neurons could be modeled as simple logical elements that take binary inputs and produce binary outputs. These neurons were referred to as “McCulloch-Pitts neurons” and formed the building blocks of their logical calculus.
Propositional Calculus
McCulloch and Pitts drew inspiration from propositional calculus, a branch of mathematical logic. They developed a formal system that described how logical operations, such as conjunction (AND), disjunction (OR), and negation (NOT), could be applied to the inputs and outputs of neurons to simulate neural activity.
Computational Universality
One of the significant findings of the paper was that the proposed logical calculus was computationally universal. This means that any computable function could be represented using a network of McCulloch-Pitts neurons and appropriate connections.
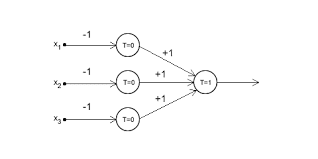
Connectionism and Neural Networks
McCulloch and Pitts explored the idea that complex cognitive processes could emerge from simple interconnected neurons. They discussed how networks of these neurons, with weighted connections and feedback loops, could exhibit behaviors similar to information processing in the brain.
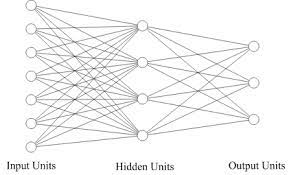
Implications for Neuroscience and AI
The paper had profound implications for both neuroscience and artificial intelligence. It provided a formal framework for understanding neural computation and inspired further research in the field of neural networks, leading to the development of more sophisticated models and algorithms.
Overall, “A Logical Calculus of the Ideas Immanent in Nervous Activity” laid the foundation for understanding neural computation and sparked the field of neural networks, which has had a significant impact on various disciplines, including neuroscience, cognitive science, and machine learning.